Java符号运算

先给大家晒一晒代码

import cn.hutool.core.util.HexUtil;

String hex = "1f8698690e02ca16618550ef7f19da8e945b555a";
byte[] hexByte = HexUtil.decodeHex(hex);
int bin_code = (hexByte[10]  & 0x7f) << 24
		| (hexByte[11] & 0xff) << 16
		| (hexByte[12] & 0xff) <<  8
		| (hexByte[13] & 0xff);

bin_code = bin_code % (int)Math.pow(10,6);

看到这段代码，大家什么感受。

尤其平时大家在翻阅源码时，这样的代码更是屡见不鲜。

是不是脑袋已经泛起了涟漪。小小的脑袋里面，充满了大大的问号？

这是个什么东东，是什么运算，运算过程是什么，运算结果又是什么样的。

今天我们就来好好探究探究里面的秘密。

其实这些运算都是对数据的二进制进行运算。

感觉难理解是因为我们最直观的是十进制，对于二进制我们需要脑袋里面先进行转换，将十进制切换到二进制再进行运算，就有点绕弯弯。

那我们换种思路呢，我们抛弃掉十进制。

当呈现在我们眼前的就是直观的二进制，然后我们再进行运算，会不会清晰明了很多。

话不多说，我们动手来实践一下。

逻辑符

在进行运算符之前，我们先看两个简单的逻辑符。

&&（逻辑与）

&&逻辑规则是只有所有的表达式结果都是 true，结果才是 true，只要存在 false，结果就是 false。

逻辑与会从左边的表达式开始计算，只要存在 false，结果就是 false。后续不管多少表达式，均不再计算，第一个为 true，再依次计算右边的表达式，当所有的表达式都为 true，结果才是true。

我们用代码说明一下。

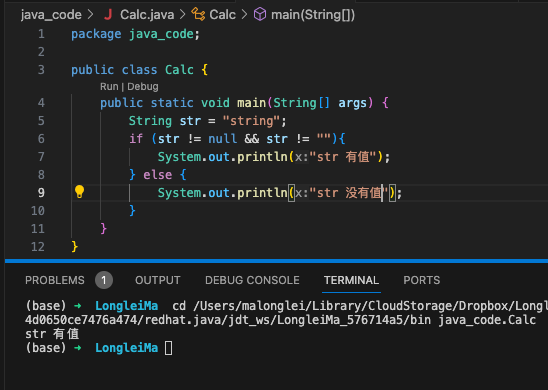
||（逻辑或）

||逻辑规则是只要有一个表达式为 true，结果就为 true，只有当所有表达式都为 false，结果才是false。

逻辑或也会从左边的表达式开始计算，只要存在 true，结果就是 true。后续不管多少表达式，均不再计算，第一个为 false，再依次计算右边的表达式，当所有的表达式都为 false，结果才是false。

代码说明一下。

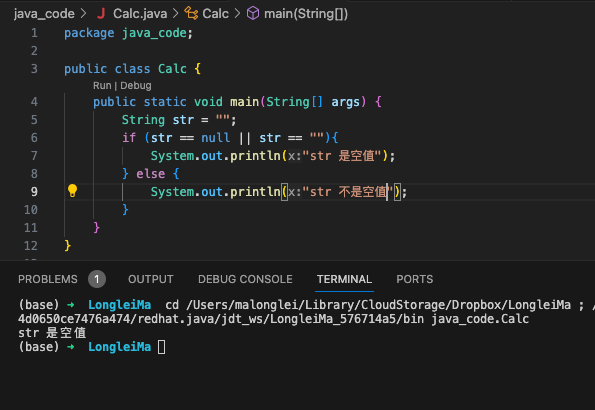
不就是二进制的运算嘛

说完了逻辑符，下面我们逐个对运算符进行解析

再解析之前，我们先明确一个概念，在运算中，1 代表true，0 代表false。

我们开始吧。

&（按位与）

&(按位与)的运算规则和&&(逻辑与)一致，两个都是 1/true，结果才是 1/true，否则就是 0/false，所以就是 1&1=1, 1&0=0, 0&1=0, 0&0=0

我们来看段实例:

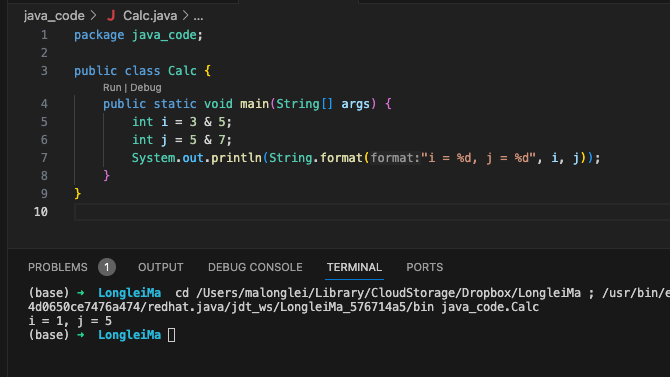
解析一下这段代码。

3 的二进制位是 0000 0011 ， 5 的二进制位是 0000 0101 ，那么 3 & 5 就是 0000 0011 & 0000 0101，由&运算规则得知，0000 0011 & 0000 0101 等于 0000 0001，转换成十进制就是 1

0000 0011 = 3
0000 0101 = 5 
3 & 5 = 0000 0011 & 0000 0101 = 0000 0001
0000 0001 = 1

5 的二进制位是 0000 0101，7 的二进制位是 0000 0111，5 & 7 就是 0000 0101 & 0000 0111 等于 0000 0101，转换成十进制就是 5

0000 0101 = 5
0000 0111 = 7
5 & 7 = 0000 0101 & 0000 0111 = 0000 0101
0000 0101 = 5

|（按位或）

|(按位或)运算规则和||(逻辑或)一致，是只要有一个为 **1(true)**，结果就为 **1(true)， **否则就是 **0(false)**，即 1|0=1, 1|1=1, 0|0=0, 0|1=1

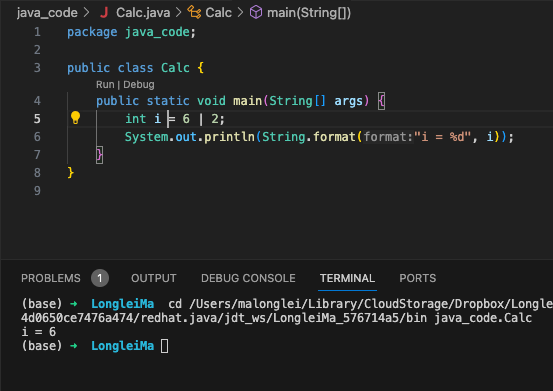
6 的二进制位 0000 0110 , 2 的二进制位 0000 0010 , 6｜2 就是 0000 0110 | 0000 0010 ，结果就是 0000 0110，转换成十进制就是 6

0000 0110 = 6
0000 0010 = 2
6 | 2 = 0000 0110 ｜ 0000 0010 = 0000 0110
0000 0110 = 6

^（异或运算符）

^异或运算符顾名思义，异就是不同，当双方不一致时，结果就是 1(true), 否则就是 0(false), 其运算规则为 1^0=1, 1^1=0, 0^1=1, 0^0=0

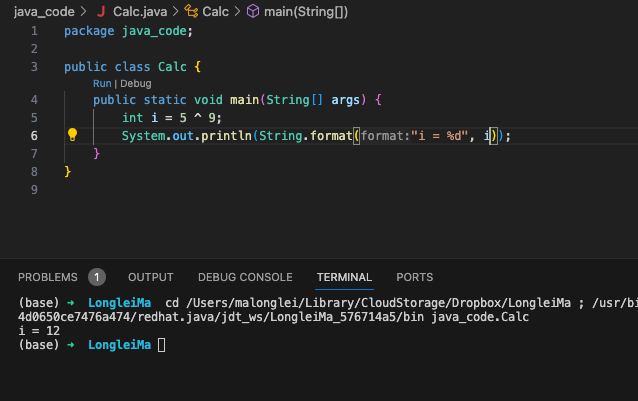
5 的二进制位是 0000 0101 ， 9 的二进制位是 0000 1001，5 ^ 9 也就是 0000 0101 ^ 0000 1001, 结果为 0000 1100 , 转换成十进制位就是 12

0000 0101 = 5
0000 1001 = 9
5 ^ 9 = 0000 0101 ^ 0000 1001 = 0000 1100
0000 1100 = 12

~（取反运算符）

~取反运算符，就是将原来的值取反，即 1(true) => 0(false)，0(false) => 1(true).

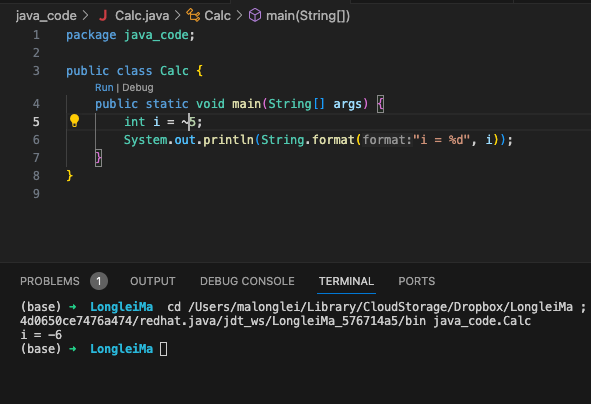
5 的二进制位是 0000 0101，取反后为 1111 1010，转换成十进制就是 -6

1
2
3

0000 0101 = 5
~5 = 1111 1010
1111 1010 = -6

<<（左移运算符）

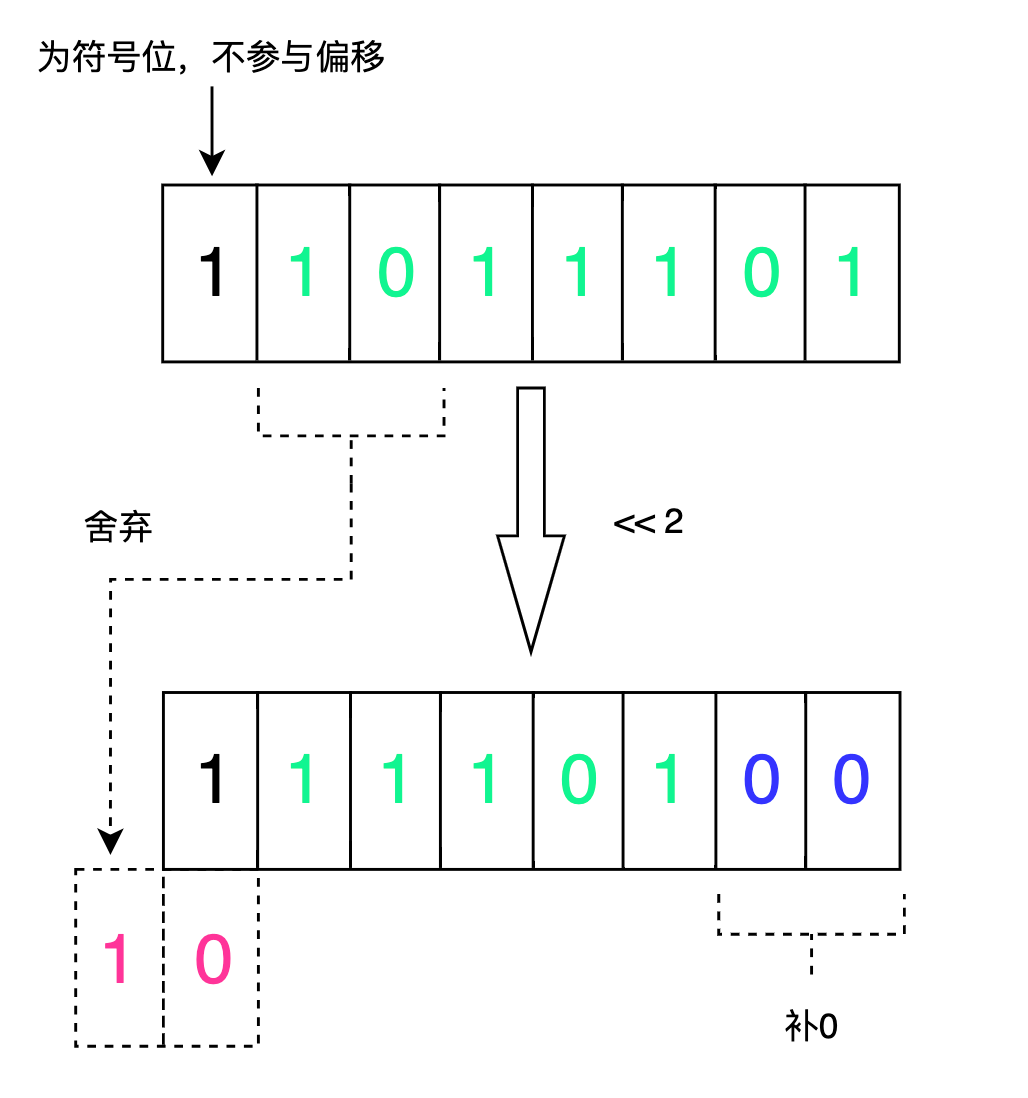
左移运算符就是整体向左偏移，左边偏移的值舍弃，右边空缺的值补0。

由于是有符号的左移，所以左边第一位是符合位，不参与偏移，左移的起始位置从第二位开始算起

画图说明一下吧。

代码实践一下。

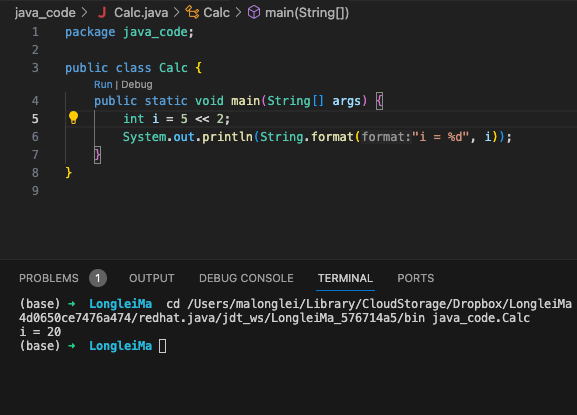
5<<2 的意思为5的二进制位往左挪两位，右边补 0，5 的二进制位是 0000 0101 ，我们排除符号位，从第二位往左挪两位, 结果就是 0001 0100, 转换成十进制就是 20

1
2
3

0000 0101 = 5
5 << 2 = 0001 0100
0001 0100 = 20

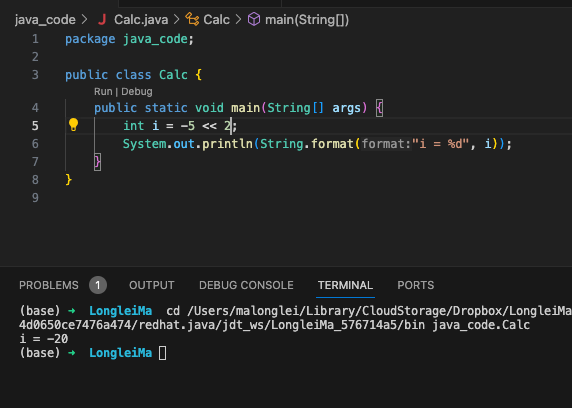
-5 二进制表示为 1111 1011，我们排除符合位，向左偏移2位，结果就是 1110 1100，转换成十进制就是 -20

1
2
3

1111 1011 = -5
-5 << 2 = 1110 1100
1110 1100 = -20

下面我们用程序看一下二进制的变化，如下图所示:

由于Integer占4个字节，所以我的截图里面，二进制长度有32位，我们只关注最后偏移的几位的变化就OK。

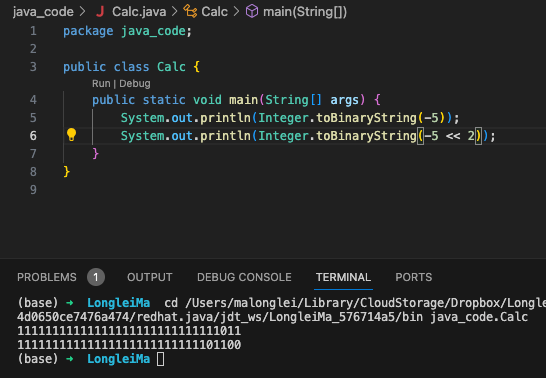
左移运算符在十进制上有个快捷的计算方式，<< n 在十进制上等于原值乘于2的n次方，例如，5 << 2 = 5 * 2² = 20, -5 << 2 = -5 * 2² = -20

>>（带符号右移运算符）

右移运算符和左移运算符相反，左移是向左移动，而右移则是向右移动。

右移运算符同样也有符合位，左边第一位是符合位，不参与偏移，右移的起始位置也是从第二位开始算起

右移运算符整体向右偏移，右边偏移的值舍弃，左边空缺的值补符合位的值，也就是说符号位是 1 就补 1，符号位是 0 就补 0，这一点与左移运算不一致。

也画图说明一下

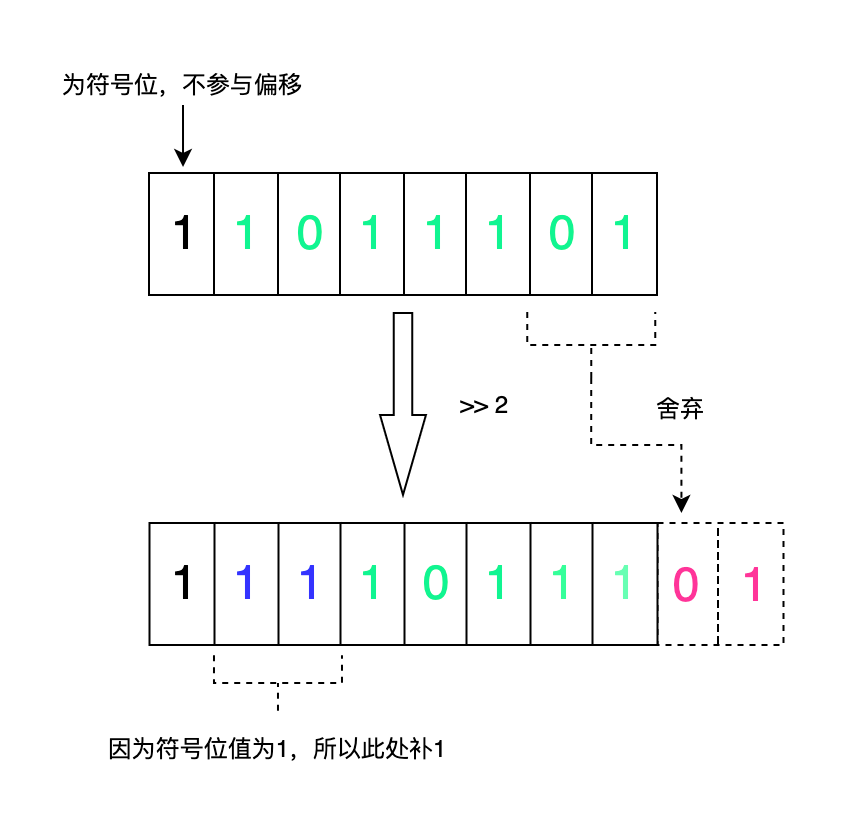
代码实践一下。

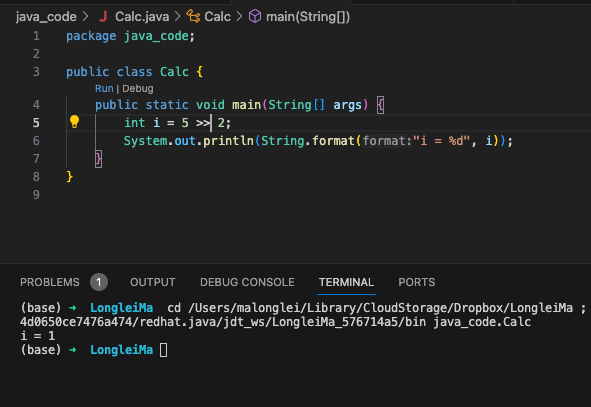
5 的二进制位是 0000 0101，右移两位后，因为符号位是 0，所以我们在前面补 0，结果就是 0000 0001，转换成十进制是 1

1
2
3

0000 0101 = 5
5 >> 2 = 0000 0001
0000 0001 = 1

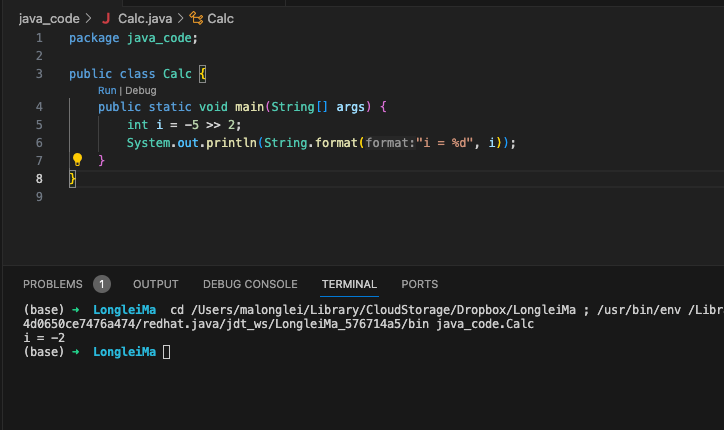
-5 的二进制位是 11111011，右移两位后，因为符号位是 1，所以我们在前面补 1，结果就是 1111 1110，转换成十进制是 -2

1
2
3

11111011 = -5
-5 >> 2 = 1111 1110
1111 1110 = -2

右移运算符在十进制上有个快捷的计算方式，

对于正数来说，>> n 在十进制上等于原值除2的n次方。
对于负数来说，>> n 在十进制上等于原值除2的n次方的基础上，如果余数等于0，则保持不变，如果余数不等于0，则结果 -1。

例如:

5 >> 2 = 5 / 2² = 1

-8 >> 2 = -8 / 2² = -2…0 = -2

-11 >> 2 = -11 / 2² = -2…-3 = -2 - 1 = -3

>>>（无符号右移运算符）

>>>无符号右移运算符和>>右移运算符的主要区别在于符号位的计算。

无符号右移运算符，符号位也参与偏移，左边空缺的值不是补符号位，而是统一补0

画图说明一下

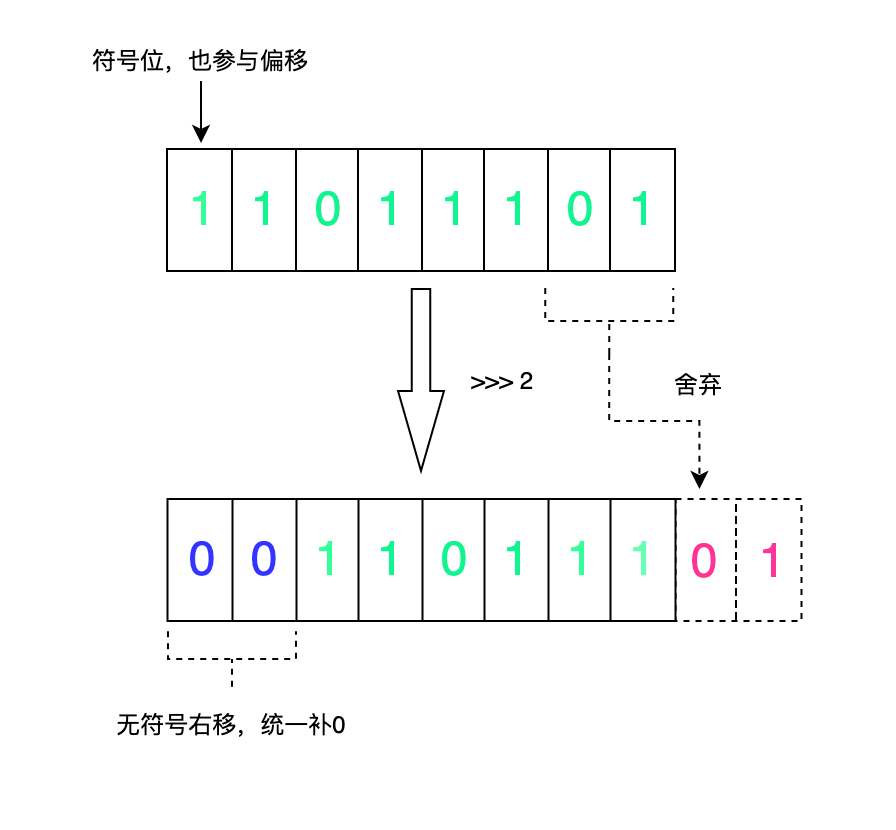
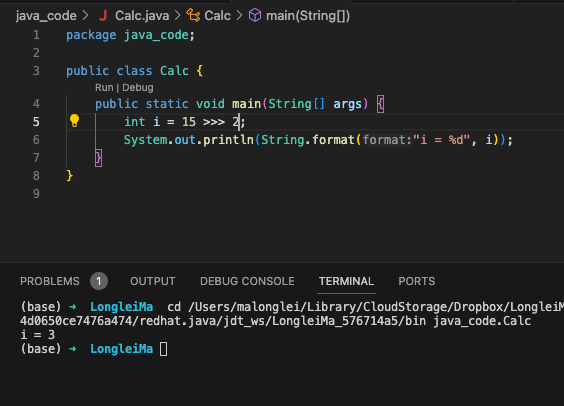
15 的二进制位是 0000 1111 ，右移2位，左边统一补0，结果就是 0000 0011，转换成十进制就是 3

1
2
3

0000 1111 = 15
15 >>> 2 = 0000 0011
0000 0011 = 3

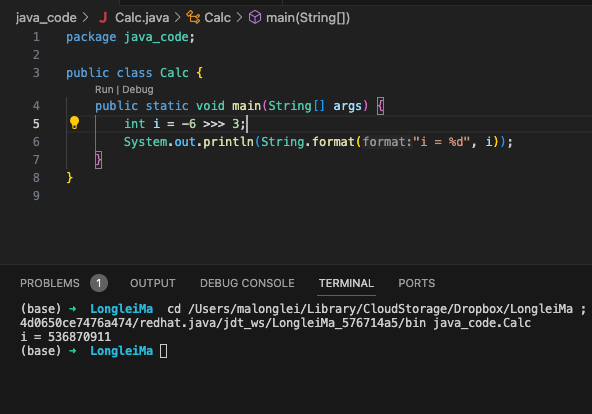
-6 的二进制是 11111111 11111111 11111111 11111010 右移三位 00011111 11111111 11111111 11111111

这里为什么不在用8位表示，而是32位表示呢，因为符号位也参与了偏移，在计算机中，int类型占4个字节，为了保持结果一致，这里我们采用32位来表示。

// 在java中int占4个字节
11111111 11111111 11111111 11111010 = -6
-6 >>> 3 = 00011111 11111111 11111111 11111111
00011111 11111111 11111111 11111111 = 536870911

重温一遍位移运算符

上面我们已经讲了 <<、>>、>>> 三个运算符号，下面我们再结合程序，以及画图展示再重温一遍。
如果你认为你已经掌握了这三个运算符，可以忽略本小节

左移操作符 <<

左移操作符 << 是将数据转换成二进制数后，向左移若干位，高位丢弃，低位补零。

看如下例子：

public static void main(String[] args) {
	int i1 = -1;
	System.out.println("source  , binary string is " + Integer.toBinaryString(i1) + " \ti1's value is " + (i1));
	System.out.println("<<  10  , binary string is " + Integer.toBinaryString(i1 << 10) + " \ti1's value is " + (i1 << 10));
}

Java的int占32位，因此对i = -1转换成二进制数，然后左移10位，其结果是左边高10位丢弃，右边低10位补0，再转换为十进制，得到i = -1024的结果。

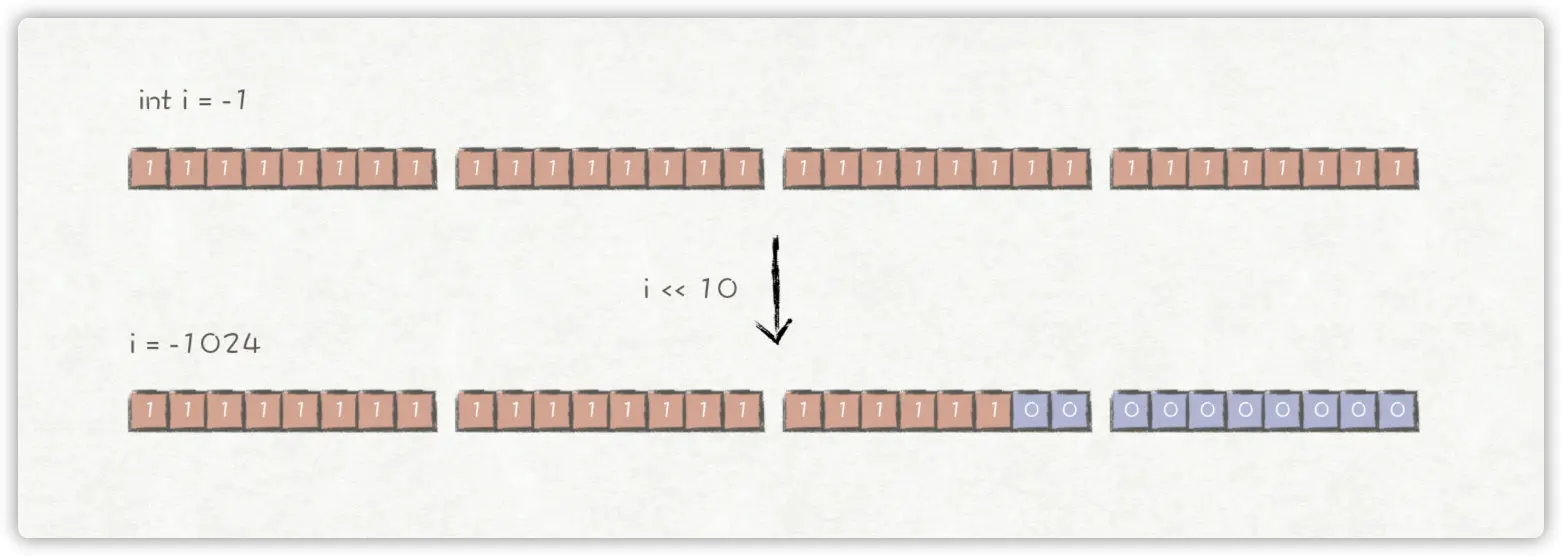
因此，上述例子的输出结果为：

1 2	source , binary string is 11111111111111111111111111111111 i1's value is -1 << 10 , binary string is 11111111111111111111110000000000 i1's value is -1024

带符号右移操作符 >>

Java中整型表示负数时，最高位为符号位，正数为0，负数为1。>> 是带符号的右移操作符，将数据转换成二进制数后，向右移若干位，高位补符号位，低位丢弃。对于正数作右移操作时，具体体现为高位补0；负数则补1。

看如下例子：

public static void main(String[] args) {
	int i1 = 4992;
	System.out.println("source  , binary string is " + Integer.toBinaryString(i1) + " \ti1's value is " + (i1));
	System.out.println(">>  10  , binary string is " + Integer.toBinaryString(i1 >> 10) + " \ti1's value is " + (i1 >> 10));
	int i2 = -4992;
	System.out.println("source  , binary string is " + Integer.toBinaryString(i2) + " \ti2's value is " + (i2));
	System.out.println(">>  10  , binary string is " + Integer.toBinaryString(i2 >> 10) + " \ti2's value is " + (i2 >> 10));
}

例子中，i1 = 4992转换成二进制数，右移10位，其结果是左边高10位补0，右边低10位丢弃，再转换为十进制，得到i1 = 4的结果。同理，i2 = -4992，右移10位，左边高10位补1，右边低10位丢弃，得到i2 = -5的结果。

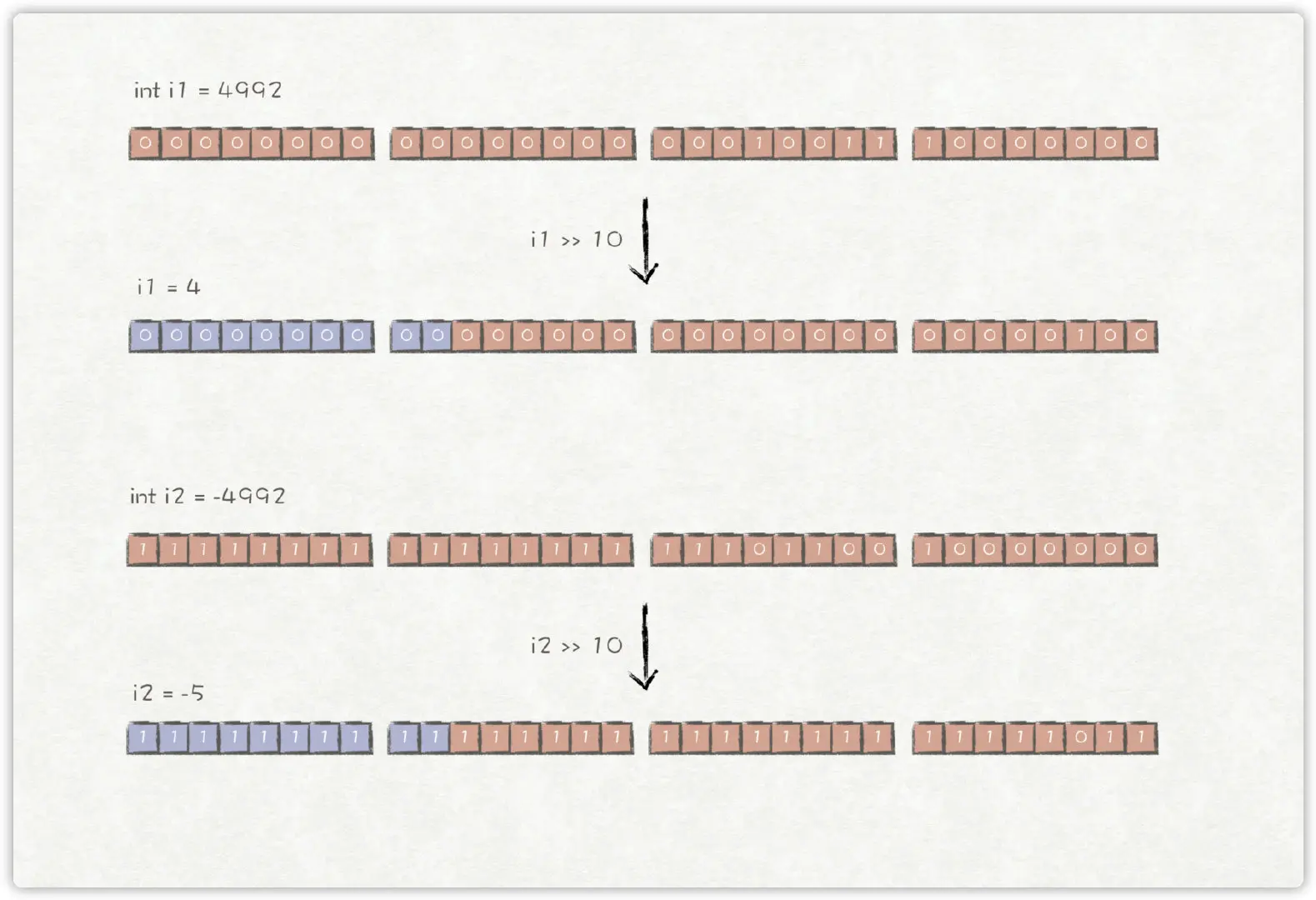
因此，上述例子的输出结果为：

source  , binary string is 1001110000000        i1's value is 4992
>>  10  , binary string is 100  i1's value is 4
source  , binary string is 11111111111111111110110010000000     i2's value is -4992
>>  10  , binary string is 11111111111111111111111111111011     i2's value is -5

无符号右移操作符 >>>

无符号右移操作符 >>>与>>类似，都是将数据转换为二进制数后右移若干位，不同之处在于，不论负数与否，结果都是高位补零，低位丢弃。

看如下例子：

public static void main(String[] args) {
	int i3 = -4992;;
	System.out.println("source  , binary string is " + Integer.toBinaryString(i3) + " \ti3's value is " + (i3));
	System.out.println(">>> 10  , binary string is " + Integer.toBinaryString(i3 >>> 10) + " \ti3's value is " + (i3 >>> 10));
}

同样对i3 = -4992进行操作，转换成二进制数后，右移10位，其结果为左边高10位补0，右边低10位丢弃，再转换成十进制，得到i3 = 4194299的结果。

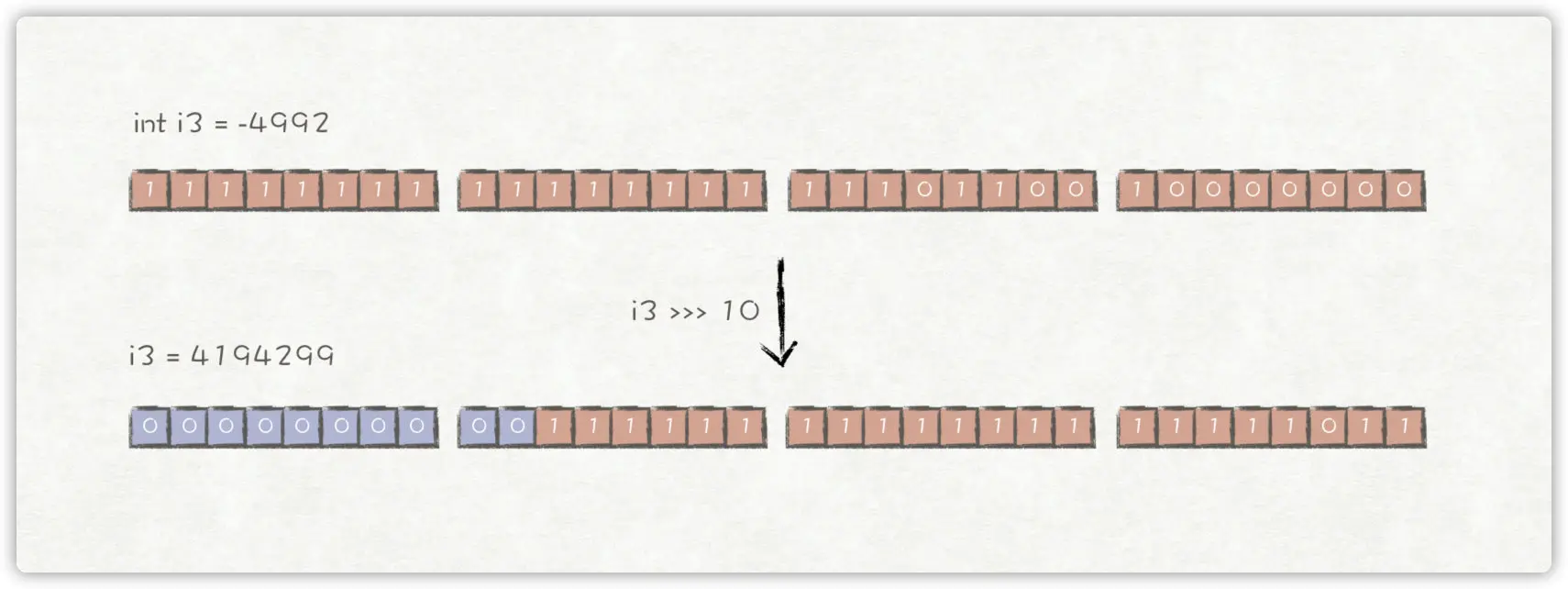
因此，上述例子的输出结果为：

1 2	source , binary string is 11111111111111111110110010000000 i3's value is -4992 >>> 10 , binary string is 1111111111111111111011 i3's value is 4194299

真的懂了吗？

对 short、byte、char 的移位操作

再看如下例子：

public static void main(String[] args) {
	byte b = -1;
	System.out.println("source  , binary string is " + Integer.toBinaryString(b) + " \tb's value is " + (b));
	b >>>= 6;
	System.out.println(">>>  6  , binary string is " + Integer.toBinaryString(b) + " \tb's value is " + (b));
}

Java的byte占8位，按照前面讲述的原理，对b = -1转换为二进制数后，右移6位，左边高6位补0，右边低位丢弃，其结果应该是b = 3。

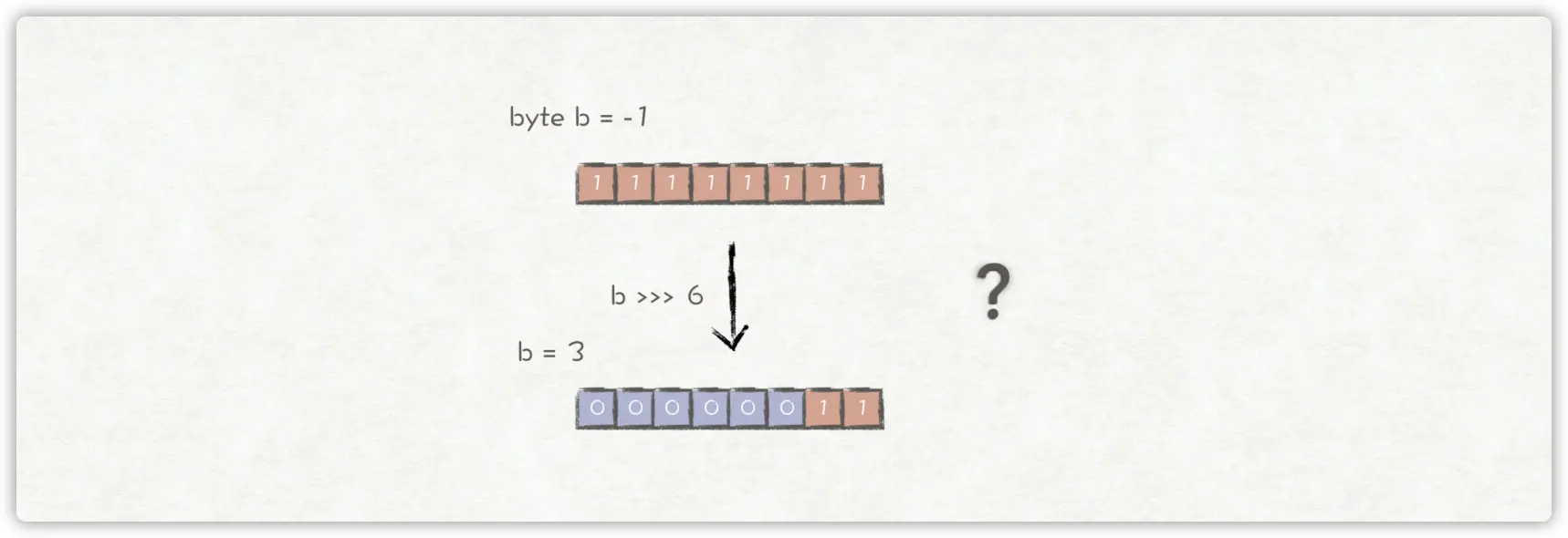
真的这样吗？我们看一下例子运行的结果：

1 2	source , binary string is 11111111111111111111111111111111 b's value is -1 >>> 6 , binary string is 11111111111111111111111111111111 b's value is -1

运行结果与我们预期的结果不对！

原来，Java在处理byte、short、char的移位操作前，会先将其转型成int类型，然后在进行操作！特别地，当对这三者使用<<=、>>=和>>>=时，其实是得到对移位后的int进行低位截断后的结果！对例子改动一下进行验证：

public static void main(String[] args) {
	byte b = -1;
	System.out.println("source  , binary string is " + Integer.toBinaryString(b) + " \tb's value is " + (b));
	System.out.println(">>>  6  , binary string is " + Integer.toBinaryString(b >>> 6) + " \tb's value is " + (b >>> 6));
}

在该例子中，没有使用 >>>= 对 b 进行再赋值，而是直接将 b >>> 6 进行输出（需要注意的是，b >>> 6 的结果为 int 类型），其输出如下：

1 2	source , binary string is 11111111111111111111111111111111 b's value is -1 >>> 6 , binary string is 11111111111111111111111111 b's value is 67108863

因此，第一个例子中实际的运算过程应该是这样：

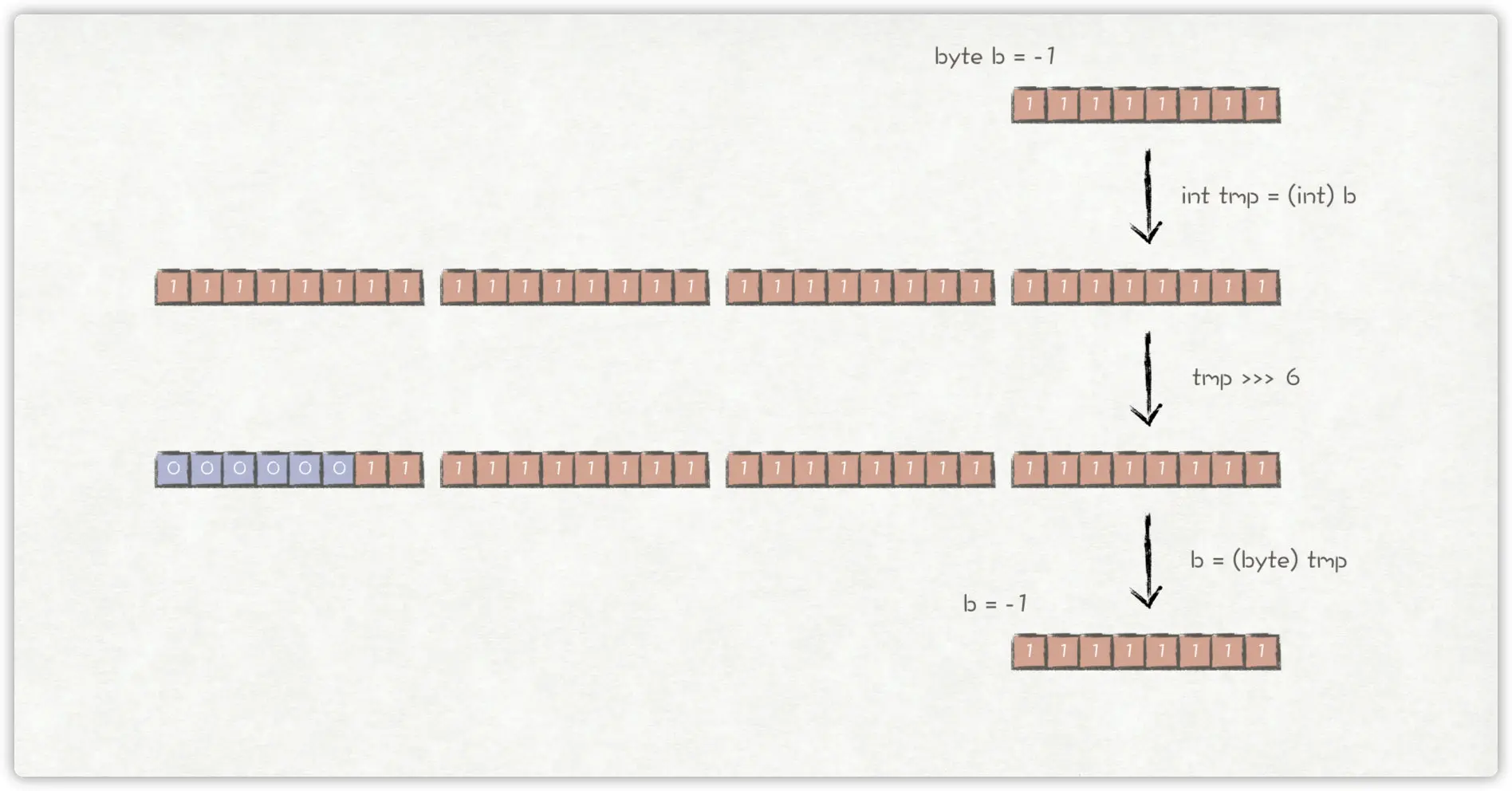
对于short和char的移位操作原理也一样，读者可以自行进行实验验证。

冒出了一个好问题

如果移位位数超过数值占有的位数会怎样?

到目前为止的所有的例子中，移位的位数都在数值所占有的位数之内，比如对int类型的移位都没有超过32。那么如果对int类型移位超过32位会怎样？

且看如下例子：

public static void main(String[] args) {
	int i4 = -1;
	System.out.println("source  , binary string is " + Integer.toBinaryString(i4) + " \ti4's value is " + (i4));
	System.out.println(">>> 31  , binary string is " + Integer.toBinaryString(i4 >>> 31) + " \ti4's value is " + (i4 >>> 31));
	System.out.println(">>> 32  , binary string is " + Integer.toBinaryString(i4 >>> 32) + " \ti4's value is " + (i4 >>> 32));
	System.out.println(">>> 33  , binary string is " + Integer.toBinaryString(i4 >>> 33) + " \ti4's value is " + (i4 >>> 33));
}

根据前面讲述的原理，对于i4 >>> 31我们很容易得出结果为1。

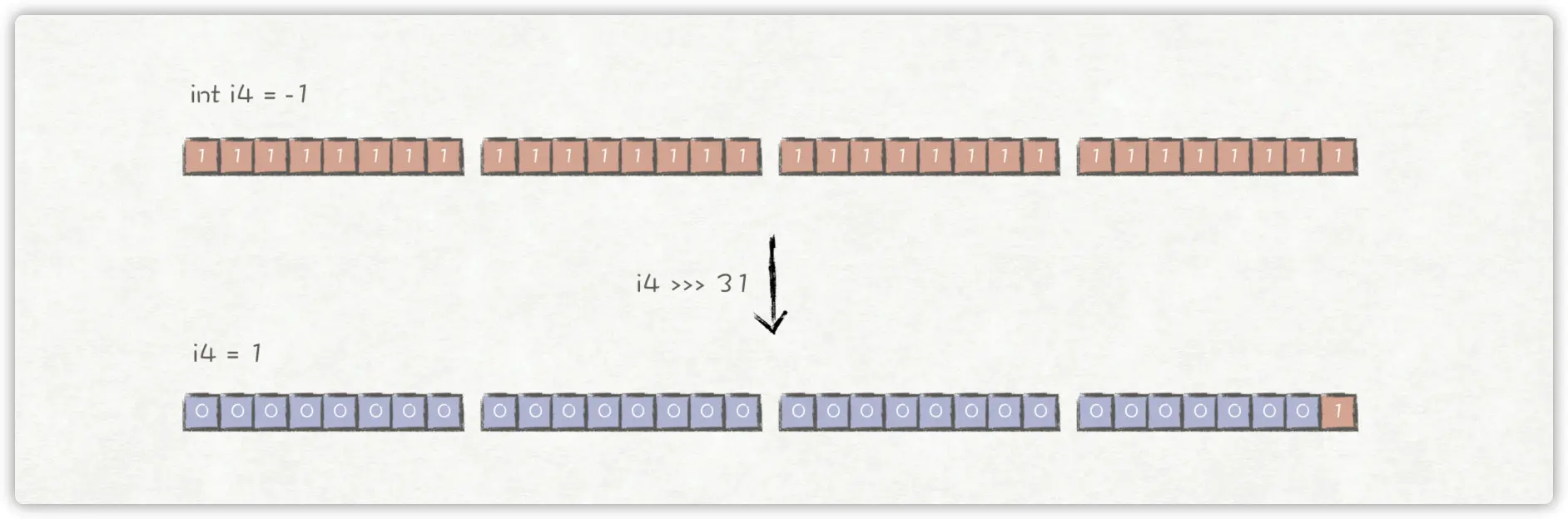
那么，i4 >>> 32的结果会是0吗？

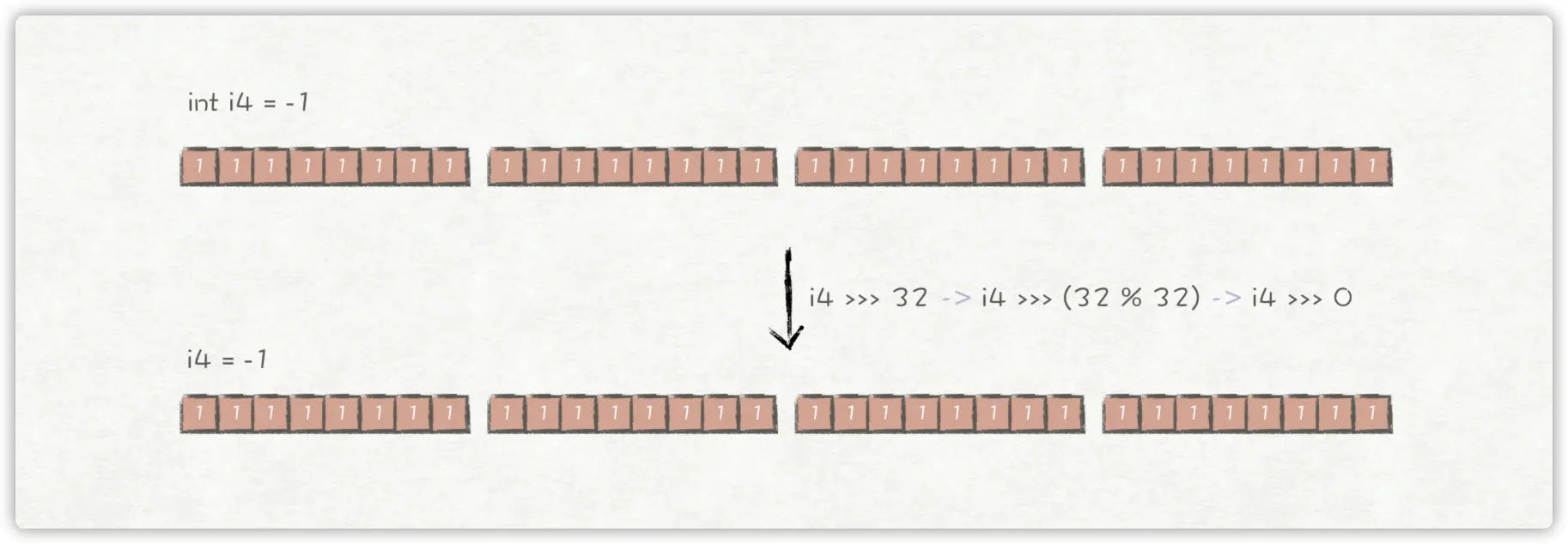
NO！Java对移位操作符的右操作数rhs有特别的处理，对于int类型，只取其低5位，也就是取rhs % 32的结果；对于long类型，只取其低6位，也即是取rhs % 64的结果。因此，对于i4 >>> 32，实际上是i4 >>> (32 % 32)，也即i4 >>> 0，结果仍然是-1。

同理，对于i4 >>> 33等同于i4 >>> 1，其结果为2147483647。

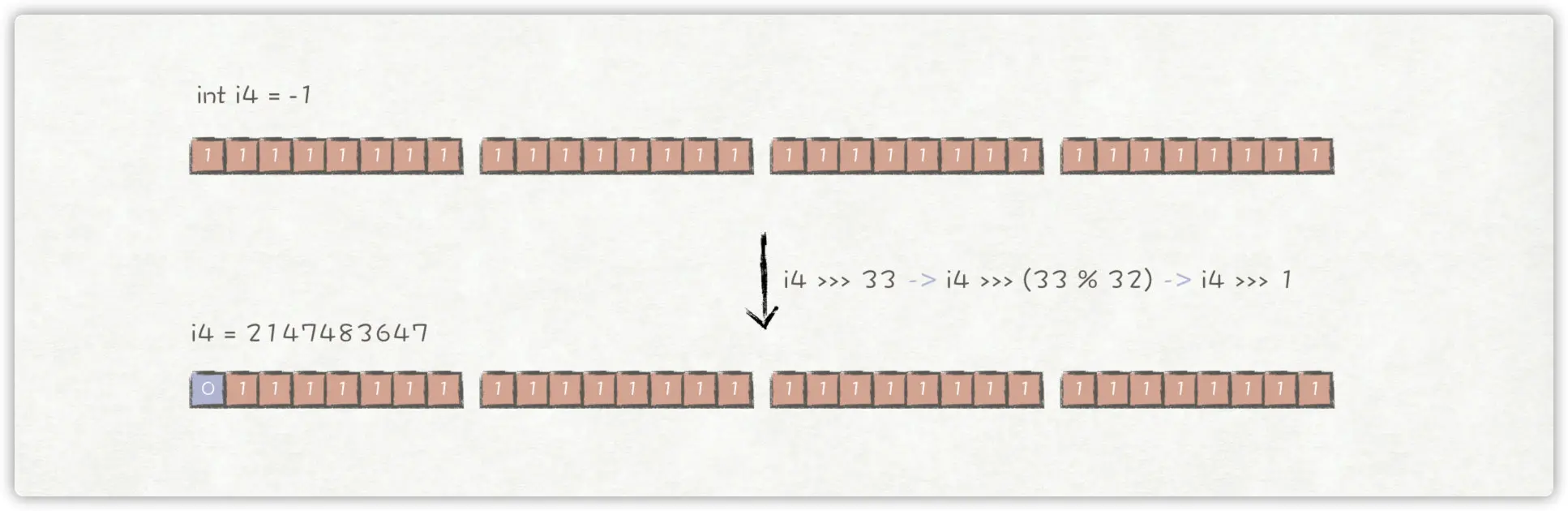
因此，上述例子的输出结果如下：

source  , binary string is 11111111111111111111111111111111 	i4's value is -1
>>> 31  , binary string is 1 	i4's value is 1
>>> 32  , binary string is 11111111111111111111111111111111 	i4's value is -1
>>> 33  , binary string is 1111111111111111111111111111111 	i4's value is 2147483647

对于long类型也是同样的道理，读者可以自行进行实验验证。

再看示例代码

现在我们对符号的运算操作有了一定的认知了，也明白了之间的运算逻辑。

那我们后过头来，重新看一下我们开头抛出的代码，大家不用往回翻了，下面我重新写一遍。

import cn.hutool.core.util.HexUtil;

String hex = "1f8698690e02ca16618550ef7f19da8e945b555a";
byte[] hexByte = HexUtil.decodeHex(hex);
int bin_code = (hexByte[10]  & 0x7f) << 24
		| (hexByte[11] & 0xff) << 16
		| (hexByte[12] & 0xff) <<  8
		| (hexByte[13] & 0xff);

bin_code = bin_code % (int)Math.pow(10,6);

大家可以先自己演算一下过程，然后再来看我的过程。

现在给大家几分钟。

好了，我们继续。

首先来看一下 hex 变量

hex 变量就是一个hex(十六进制)的字符串,我们直接转换成对应的二进制，来看一下它的真实面貌。

下面就是它二进制的信息，总共有20个字节长度。

-------------------------------------------------------------------------------------------
|0        1        2        3        4        5        6        7        8        9       |
-------------------------------------------------------------------------------------------
|00011111 10000110 10011000 01101001 00001110 00000010 11001010 00010110 01100001 10000101|
-------------------------------------------------------------------------------------------
|10       11       12       13       14       15       16       17       18       19      |
-------------------------------------------------------------------------------------------
|01010000 11101111 01111111 00011001 11011010 10001110 10010100 01011011 01010101 01011010|
-------------------------------------------------------------------------------------------

接下来我们看他第一个表达式

1	(hexByte[10] & 0x7f) << 24

hexByte[10] ,我们从上面二进制先拿到索引为10的字节，也就是 01010000，0x7f转换成十进制是127，对应的二进制是 01111111

由此

1	(hexByte[10] & 0x7f) = 01010000 & 01111111 = 01010000

然后我们在进行左移操作，上面讲左移的时候有提到过，java中，会将byte先转成int，也就是我们得先将1个字节，扩充到4个字节，再进行左移操作。

1
2
3

01010000 << 24 = 
00000000 00000000 00000000 01010000 << 24 = 
01010000 00000000 00000000 00000000 = 1342177280

接下来我们看他第二个表达式

逻辑和上面一致，所以我这里简化一下，只展示一下运算过程。

(hexByte[11] & 0xff) << 16
↓
11101111  & 255 = 11101111 & 11111111 = 11101111
↓
11101111 << 16 = 
00000000 00000000 00000000 11101111 << 16 = 
00000000 11101111 00000000 00000000 = 15663104

接下来我们看他第三个表达式

(hexByte[12] & 0xff) <<  8
↓
01111111  & 255 = 01111111 & 11111111 = 01111111
↓
01111111 << 8 = 
00000000 00000000 00000000 11101111 << 8 = 
00000000 00000000 01111111 00000000 = 32512

接下来我们看他第四个表达式

(hexByte[13] & 0xff)
↓
00011001  & 255 = 00011001 & 11111111 = 
00011001 = 
00000000 00000000 00000000 00011001 = 25

运算完 & 和 << 后，我们再运算 | 运算，如下

01010000 00000000 00000000 00000000 |
00000000 11101111 00000000 00000000 | 
00000000 00000000 01111111 00000000 |
00000000 00000000 00000000 00011001 
=
01010000 11101111 01111111 00011001 = 1357872921